11. Step 11: Assess risk and uncertainty
Steps
11.1 Undertake simple sensitivity analyses.
11.2 Decide on the level of detail for a risk analysis.
11.3 Identify risky variables and sources of risk.
11.4 Assign alternative values to risky variables.
11.5 Assign probabilities to events.
11.6 Identify states of nature and associated probabilities.
11.7 Calculate expected values of CBA results.
11.8 Calculate probability-based values of investment costs if required.
11.9 Use a computer program if the analysis becomes too complicated.
11.10 Consider risk management strategies.
All benefits and costs that go into a CBA are forecasts of the future. Risk and uncertainty arise from the possibility that a forecast will prove to be wrong.
Distinguish between downside risk and pure risk. Downside risk arises because people usually do not to consider what can go wrong, causing assessments to be biased in favour of the initiative. If downside risk has been eliminated from projections, the remaining variation about the expected value is called pure risk. In most cases, pure risk can be ignored in CBAs. See NGTSM Volume 5, Section 2.11 or BTRE (2005) for an explanation.
For financial analyses, the weighted average cost of capital will include a risk premium. It compensates lenders and shareholders for bearing the risk that the firm will go bankrupt. It is not a mechanism to offset optimism bias in financial calculations.
It is not good practice to add a risk premium to the discount rate for CBAs. It can distort ranking of initiatives. See NGTSM 2006 Volume 5, Section 2.11 or BTRE (2005) for an explanation.
11.1 Undertake simple sensitivity analyses
Sensitivity analysis is a simple way to analyse the uncertainty surrounding CBA results, but it is a limited tool. In its most basic form, it involves changing one variable at a time by a standard percentage, say, +10 per cent followed by –10 per cent, or by an absolute amount to gauge how much NPV changes. If the NPV changes by only a small amount (e.g. ±10 per cent change causes a ±3 per cent change in NPV), it implies that the uncertainty surrounding the variable is not very important and is not critical to decision-making. Conversely, if the affect on NPV is large in percentage terms, the robustness of the CBA can be called into question. It may be worthwhile to expend more resources to obtain a better estimate of the variable, though this will do nothing to reduce risk arising from inherent volatility of the variable.
Choose the percentage variations used for sensitivity tests, bearing in mind the range of plausible values that a variable can take. The amounts the variables change by do not have to be symmetrical.
As an example, Table 3 shows the sensitivity ranges for road initiatives recommended by Austroads.
| VARIABLE | SUGGESTED MINIMUM VALUE | SUGGESTED MAXIMUM VALUE |
|---|---|---|
| Capital costaConcept estimateDetailed costingFinal costing | –20% of estimate –15% of estimate –10% of estimate |
+20% to 35% of estimateb +15% to 25% of estimateb +10% to 20% of estimateb |
| Road-agency operating and maintenance costs | –10% of estimate | +10% of estimate |
| Traffic Total traffic volume (AADT) Proportion heavy vehicles Average car occupancy Traffic growth rate Traffic generated by specific (uncertain) developments Traffic diverted or generated by the initiative Traffic speed changes Changes in crash rates |
–10% to –20% of estimate –5 percentage points –0.3 from estimate –2% pa (absolute) from the forecast rate Zero – 50% of estimate –25% of estimated change in speed –50% of estimated change |
+10% to +20% of estimate +5 percentage points +0.3 from estimate +2% pa (absolute) to the forecast rate As forecast +50% of estimate +25% of estimated change in speed +50% of estimated change |
a. The appropriate range for capital costs depends on the detail of investigations, designs and costing.The concept estimate relates to initial pre-feasibility or sketch-planning estimates. The final costing relates to estimates after the final design stages.
b. The range of values relates to different types of initiative. Costing for more routine initiatives (e.g. road shape correction, resealing) are generally more accurate than those for larger initiatives (e.g. new motorway construction). Source: Austroads 1996, p. 28; and 2005a, p. 27.
Spreadsheets are ideally suited to conducting sensitivity tests. Group the list of parameters likely to be tested in an easily accessed part of the spreadsheet (for example, the upper left corner). Present the results in terms of percentage and/or absolute deviations in NPV and BCR in a table.
11.2 Decide on the level of detail for a risk analysis
The SMT and rapid CBA template (see Part F3 of the ATAP Guidelines) requires proponents to address a series of questions about the risks of their proposed initiatives. Some of these relate to risks that the initiative will be delayed. There is a question about describing the major risks on the cost side (e.g. excess costs) and benefit side (e.g. where benefits are not realised). For the SMT and rapid CBA, it is not necessary to go further by conducting a state-contingent assessment as described here.
For detailed CBAs of larger initiatives, governments may insist on a probabilistic analysis, at least for investment costs, which may require the use of computer software. The larger the initiative, the greater the level of detail warranted. Discuss the level of detail required with the government agency assessing the proposal.
The remainder of this section is concerned with the probabilistic approach. This approach helps to minimise downside risk or optimism bias, that is, to ensure that the results of CBAs are expected values (the means of probability distributions). It provides a thought process that disciplines the analyst to ask a complete set of ‘what if?’ questions.
11.3 Identify risky variables and sources of risk
The main sources of risk for investment initiatives are:
- Construction costs that differ from the expected because of changes in input costs or unforeseen technical factors
- Operating costs that differ from the expected because of changes in input costs or unforeseen technical factors
- Demand forecasts that differ from the expected, a risk that rises the further into the future the projections are made
- Environmental impacts that differ from the expected or are unforeseen
- Network effects, where an asset is part of the network (for example, an individual length of road or rail track) and decisions made elsewhere in the network impact on the initiative in question.
11.4 Assign alternative values to risky variables
Identify the possible values, or ranges of values, that risky benefits and costs (or variables affecting them) can take. Technically, each value (or range of values) that a variable can take is called an event. Wherever possible, identify circumstances associated with each event (such as equipment breakdowns, adverse weather, technical difficulties, unanticipated environmental or planning requirements, industrial disputes and population levels).
Be wary of simply assuming a symmetrical probability distribution around the estimated value of a variable. This presupposes that the estimate is the central value and may not lead to proper consideration of sources of optimism bias.
It may help to prepare checklists based on experience, examine similar current or previous initiatives, hold a brainstorming session or compile historical information. An Environmental Impact Statement (EIS) should identify environmental risks. Exclude events with very small probabilities of occurring, taking into account the size of the probability and the impact on benefits or costs.
11.5 Assign probabilities to events
In most cases, it is necessary to make subjective judgments about probabilities. In some cases, historical data or engineering models can assist. For each risky variable, the probabilities of all possible events must sum to one.
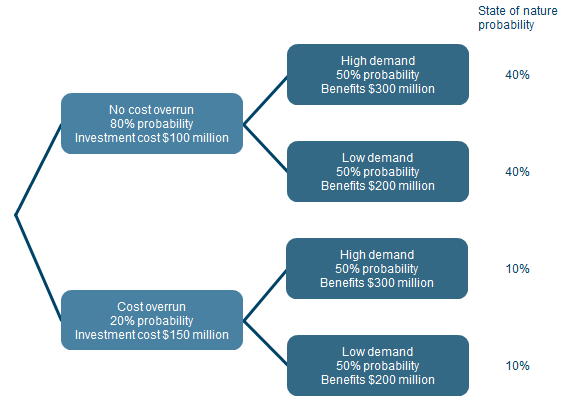
11.6 Identify states of nature and associated probabilities
Next, identify all combinations of events that can occur (technically called ‘states of nature’). Compiling an event tree can be a useful tool for this task (see Box 13). Then calculate the probability of each state of nature. The probability of a state of nature is the product of the probabilities of all the constituent events. The probabilities of all possible states of nature must sum to one.
11.7 Calculate expected values of CBA results
Each state of nature will be associated with a unique stream of year-by-year benefits and costs. Note that both the Base and Project Cases can vary in different states of nature because external factors such as the weather and economic conditions can affect both. Calculate CBA results (NPV, BCR, IRR and FYRR) for each state of nature. Multiply each result by the probability of the associated state of nature and sum to obtain expected values (see Box 13).
11.8 Calculate probability-based values of investment costs if required
Calculate probability-based values of investment costs if the funding jurisdiction requires it. Investment costs are typically reported at P50 and P90 levels. P50 and P90 are the costs with sufficient contingency to provide a 50 per cent and 90 per cent likelihood respectively that these costs will not be exceeded. With half of the area of the probability distribution on either side, P50 is the median of the probability distribution.
The central CBA scenario should have results at ‘expected values’, that is, the results should be the means of the probability distributions for the NPV and BCR. These can be obtained by ensuring that all the individual cost and benefit estimates going into the CBA are expected values. For investment costs, the P50 value or median will equal the mean or expected value of investment costs if the probability distribution is symmetrical. If the distribution is reasonably symmetrical, the P50 value can be used as an approximation of the mean for the central scenario for a CBA. The P90 value could then be used as a sensitivity test to gauge the impact of investment costs being higher than expected. It is understood that some state treasuries use the P90 estimate for budget funding purposes on the grounds that, due to optimism bias, the P90 value may be closer to the expected value than the P50 value.
For rapid CBAs and small initiatives, the ‘deterministic approach’ to costing may suffice. It involves applying a percentage contingency allowance to base estimates for either individual cost elements or to the aggregate project cost. Using the deterministic approach, the amount of the percentage contingency allowance would be quite small to approximate a P50 estimate, and relatively larger to approximate a P90 estimate (Evans and Peck, 2008, p.32). To be useful, deterministic costing requires access to reliable benchmark data, particularly at the whole-of-project level, in order to estimate the contingency allowance. Both the probabilistic and deterministic approaches to costing require input from experienced practitioners.
11.9 Use a computer program if the analysis becomes too complicated
Where the number of states of nature or the number of uncertain variables is large, the combinations of input values can become extremely large. To facilitate the process, use computer software packages such as @RISK. This software links with Excel. The program allows probability distributions for continuous variables to be specified. See Austroads (2002) for guidance.
If computer software is used to estimate expected values of CBA results, the software will also provide estimates of the variances. For public sector initiatives, variances are, in most cases, not relevant to decisions about whether initiatives should proceed or about ranking initiatives. See BTRE (2005) or NGTSM 2006 Volume 5, Section 2.11 for an explanation.
Box 13: Example of calculation of expected NPV and BCR
The present value of investment costs for a new initiative is $100 million with an 80 per cent probability, and $150 million with a 20 per cent probability if major cost overruns occur. The present value of benefits is $300 million with high demand and $200 million with low demand with a 50:50 chance of either. The diagram shows the event tree and probabilities for the four states of nature.
The table shows calculation of the expected NPV and BCR.
| Investment cost event | Cost ($m) | Demand event | Benefit (m) | Prob | NPV ($m) | Prob x NPV | BCR | Prob x BCR |
|---|---|---|---|---|---|---|---|---|
| No overrun | -100 | High | 300 | 0.4 | 200 | 80 | 3.0 | 1.2 |
| No overrun | -100 | Low | 200 | 0.4 | 100 | 40 | 2.0 | 0.8 |
| Overrun | -150 | High | 300 | 0.1 | 150 | 15 | 2.0 | 0.2 |
| Overrun | -150 | Low | 200 | 0.1 | 50 | 5 | 1.3 | 0.1 |
| Expected value | 140 | 2.3 |
11.10 Consider risk management strategies
Consider changes to proposals that can increase expected NPVs by reducing either the probabilities or the costs of adverse events. Often, these changes will involve expending additional resources with certainty (for example, building a stronger bridge). Use the probabilistic approach to assess the economic viability of each option and to compare options.
The ‘real options’ approach involves consideration of options for waiting and staged flexibility. A ‘real option’ is a decision taken today that makes it possible for policy makers to take a particular action in the future. Real options are similar to financial options but are exercised over real assets rather than financial assets (PC 2012, pp.12 and 97). Under the ‘wait and see’ approach’ options are explored that involve deferring investment until a major uncertainty is resolved or lessened and the initiative is more clearly going to be successful. Staged flexibility involves incurring additional short-term costs in exchange for lower costs later when uncertainties are resolved or lessened and decisions can be made to withdraw, proceed as planned or proceed in a different way.
The decision criterion is to choose the option that maximises the expected value of the NPV obtained from a probabilistic assessment.